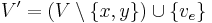Karger's algorithm

In computer science and graph theory, Karger's algorithm is a Monte Carlo method to compute the minimum cut of a connected graph. It was developed by David Karger.

1 Algorithm
2 Contraction
3 Pseudocode
4 References

Algorithm

The idea of the algorithm is based on the concept of contraction of an edge $e$ in a graph. Informally speaking, the contraction of an edge makes the two nodes joined by e overlap, reducing the total number of nodes of the graph by one. The algorithm proceeds iterating contractions until only two nodes are left in the graph. With high probability, the algorithm will return a minimal cut by returning the set of edges joining the two remaining nodes. Karger's algorithm is the fastest known minimum cut algorithm, is randomized, and computes a minimum cut with high probability in time O(|E| log³|V|).

Contraction

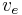Informally speaking, this operation takes an edge $e$ with endpoints $x$ and $y$ and contracts it into a new node $v_e$ which becomes adjacent to all former neighbors of $x$ and $y$ . It is possible to formalize this concept in mathematical terms.

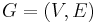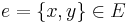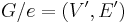Given a graph $G = \left ( V, E \right )$ and $e = \lbrace x, y \rbrace \in E$ , the contraction of $G$ respect to $e$ (written $G/e = \left ( V', E'\right )$ ) is a multigraph where:

$V' = \left( V \setminus \lbrace x, y \rbrace \right) \cup \lbrace v_e \rbrace$

and:

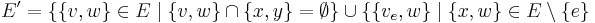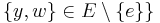
$E' = \lbrace \lbrace v, w \rbrace \in E \mid \lbrace v,w \rbrace \cap \lbrace x,y \rbrace = \emptyset \rbrace \cup \lbrace \lbrace v_e,w \rbrace \mid \lbrace x,w \rbrace \in E \setminus \lbrace e \rbrace$ or $\lbrace y,w \rbrace \in E \setminus \lbrace e \rbrace \rbrace$

It is possible to prove that this operation doesn't reduce the cardinality of the minimum cut, but that it might increase it.

Pseudocode

The algorithm can be implemented using two functions:

 function Karger(G, K)
 min := 
 for i = 1 to K do
   t := Full_contraction(G)
   if t < min then
     min := t
 return min

 function Full_contraction(G)
 for i := 1 to |V| - 2 do
   e := Random()
   G' = ( V', ') := 
   V := V'
    := '
 return ||

The function Full_contraction implements the contraction of the edges following the given definition. The iteration lasts until only two nodes are left in the graph. With a certain probability, the set of edges left are the minimum cut. It is not sure anyway that this algorithm returns a cut which is minimum, therefore K execution of Full_contraction is performed by the Karger function, where K has to be passed as a parameter. Computing the minimum of the K executions reduces the probability of having a wrong minimum cut returned.

References

David R. Karger, Global Min-cuts in RNC and Other Ramifications of a Simple Mincut Algorithm. Proceedings of the 4th Annual ACM-SIAM Symposium on Discrete Algorithms, January 1993
David R. Karger and Clifford Stein, A New Approach to the Minimum Cut Problem. Journal of the ACM 43(4):601-640, 1996

Karger's algorithm

Contents

Algorithm

Contraction

Pseudocode

References